Loop to Constant Computation
int optimize_it(int c, int n) { while (c < n) { c = c + 3; } return c; }
In this article we will see how LLVM constant-folds the loop above, why the optimization works and we will take a sneak peak at the passes that achieve that. The ASM ouputs are x86_64 but the optimizations we discuss are not (in fact, they're target-independent).
I think it is useful to see how different compilers optimize the same input. Especially when the code is small and the ASM output is mostly comprehensible. The results below are with -O1 (note that -O1 is not the same in all compilers) plus some discussion for higher levels of optimization.
test:
mov eax, edi
cmp edi, esi
jge .L2
.L3:
add eax, 3
cmp esi, eax
jg .L3
.L2:
ret
GCC at -O1 doesn't do anything fascinating.
The only thing that happened is that the loop was effectively converted to a do-while loop (i.e. it was
rotated, observe that the check happens at the "bottom" of the loop). Same at -O2.
At -O3 (Godbolt snippet) it went crazy. I didn't try to decode all the output, but the idea seems to be that first it does a bunch of (runtime) checks to see if it can unroll the loop (i.e. if there is an upper bound) and if so it branches there:
.L3:
lea eax, [rdi+3]
cmp esi, eax
jle .L1
lea eax, [rdi+6]
cmp esi, eax
jle .L1
lea eax, [rdi+9]
cmp esi, eax
jle .L1
lea eax, [rdi+12]
cmp esi, eax
jle .L1
lea eax, [rdi+15]
cmp esi, eax
jle .L1
lea eax, [rdi+18]
cmp esi, eax
jle .L1
lea eax, [rdi+21]
add edi, 24
cmp esi, eax
cmovg eax, edi
ret
And if not, it uses a vectorized version of the loop:
.L4:
movdqa xmm0, xmm1
add eax, 1
paddd xmm1, xmm3
paddd xmm0, xmm2
cmp ecx, eax
jne .L4
Still, the computation is not constant.
test:
cmp ecx, edx
jge $LN2@test
sub edx, ecx
mov eax, -1431655765 ; aaaaaaabH
dec edx
mul edx
shr edx, 1
lea eax, DWORD PTR [rcx+rdx]
lea ecx, DWORD PTR [rdx*2+3]
add ecx, eax
$LN2@test:
mov eax, ecx
ret 0
MSVC has the same output at -O1, -O2 and -Os. And it's
a good one. It has done something similar to what we'll later see LLVM doing and it effectively has converted the loop to a constant computation.
test:
jmp ..B1.9 # Prob 100%
..B1.3: # Preds ..B1.9
add edi, 3
..B1.9: # Preds ..B1.1 ..B1.3
cmp edi, esi
jl ..B1.3 # Prob 82%
mov eax, edi
ret
ICC's -O1 is similar to GCC and it's pretty basic. It has converted the loop to a do-while loop too
but in a different way. Here there's no "guard". That is, in GCC's output, there's a guard (imagine an if that
wraps the do-while loop) that verifies whether the loop will be entered at least once.
ICC has converted it to a do-while loop but jumps straight to the comparison. In C, it's like this:
int test(int c, int n) { goto cond; do { c = c + 3; cond: } while (c < n); return c; }
At -O2 (Godbolt snippet) the output is better. It uses the same ideas as MSVC above and what we'll see in LLVM to convert the loop to a constant computation.
test:
cmp edi, esi
jge ..B1.3 # Prob 50%
mov eax, 1431655766
lea ecx, DWORD PTR [1+rdi]
sub esi, ecx
add esi, 3
imul esi
sar esi, 31
sub edx, esi
lea esi, DWORD PTR [3+rdx+rdx*2]
lea edi, DWORD PTR [-3+rdi+rsi]
..B1.3: # Preds ..B1.2 ..B1.1
mov eax, edi
ret
Don't get fooled with these DWORD PTR [], they're not dereferences. It's just the syntax of lea
(which does not impose them in general, it depends on the assembler). Before moving on, I should mention that the -O3 output is the same.
Clang 10 at -O1 outputs the following (Godbolt snippet) which
is the same for all the other levels. It's a constant computation but it seems to be smaller than both ICC's and MSVC's output.
test: # @test
cmp esi, edi
cmovl esi, edi
sub esi, edi
add esi, 2
mov eax, 2863311531
imul rax, rsi
shr rax, 33
lea eax, [rax + 2*rax]
add eax, edi
ret
Interestingly, it outputs this from version 3.4.1 (Godbolt snippet).
Let's first consider a simpler version of this loop:
int test(int c, int n) { int c = 0; while (c < n) { c = c + 1; } return c; }
For that it's pretty obvious that we can compute in constant time. Note that we care for the value of c
at the end of the loop (i.e. its exit value) and that is obviously n if n > 0 or 0 otherwise.
One other way to express that is that the exit value of c is
exit_value_of_c = max(n, 0);
Now, let's do a small modification. Let's change the step from 1 to 2:
int test(int c, int n) { int c = 0; while (c < n) { c = c + 2; } return c; }
It seems that we can still compute it in constant time, but now there are more cases to consider since we may end up on n
or we may not. To put it differently, consider that in the previous version, starting from 0 and going upwards by only 1
(and assuming n > 0), it was sure that we would end up on n which made it easy
to figure out the exit value of c.
However now, if n is a multiple of 2, we'll end up on it, otherwise not. And what happens in either case?
To simplify the problem, consider that the most important thing for computing the exit value of c is the
number of iterations. If one gives us the number of iterations, it's always easy to compute
the exit value of c if we know the step, no matter what the step is (and considering it is constant).
That is because every time, we add the step to the previous value of c and thus the final value of it
should be: initial_value_of_c + number_of_iterations * step.
So, we have to find a way to generally compute the number of iterations for a given initial value of c,
a step and an n, in constant time. If we can do that, then we plug the number in the above
formula and we're done.
Back to the code with a step of 2 and let's focus on the number of iterations from now on.
If n is a multiple of 2, then the number of iterations is n / 2.
For example, for n == 4, we'll go 0 -> enter the loop, 2 -> enter the loop, 4 -> don't enter the loop.
In general, it makes sense to do exactly half n iterations.
Now, what happens when n is not a multiple of 2 ?
The idea is that in this case, n == 2k + 1 or in simple words, it is some multiple of 2 plus 1.
This is important because remember that previously, when we considered that n is a multiple of 2,
we knew that because we would end up on it, we wouldn't get in that loop iteration (e.g. 0, 2, 4 -- for 4 we don't get into the loop).
In the same manner here, starting from 0 and incrementing by 2, we will end up on 2k. But when we do,
we'll do one more iteration because of this + 1 that will let us in for one (and only one) iteration.
So, in this case, we'll do exactly n/2 + 1 iterations.
So, to sum up, if n is multiple of 2, we do n/2 iterations, otherwise,
we do n/2 + 1.
We can express that with one function, ceil().
ceil(x) gives us the ceiling of x e.g. for x = 0.5, ceil(x) = 1.
It basically accounts for that +1 iteration in the case where n is not a multiple.
Ok, we found a way to compute the number of iterations when the step is 2. How about other steps? For other steps the idea is the same.
If n is a multiple of the step, then we'll do n / step iterations. Otherwise,
n = step*k + x. That is, n is a multiple of the step plus something. But,
that something is at most step - 1, otherwise we would go to a next multiple.
So, this "plus something" is enough to give us one more iteration but only one. Which means that we generalized our formula:
number_of_iterations = ceil(n/step) + 1.
There's one last thing to consider: This works only if initial_value_of_c == 0, but it's quite
easy to generalize it. If the initial value is not 0, and is let's say v, it means we're
looping from v to n. That is the same as looping from
0 to n - v.
For example, looping from 4 to 7 is like looping from 0 to 3. It's like moving the "window" of iterations (which we can do since
we only care for the number of iterations). With this last
consideration, generally number_of_iterations = ceil((n - initial_value_of_c) / step)
That's all great and constant but ceil() in general is a floating-point function and we would like
to only use integer computations for that (note that the ASM that LLVM outputs has only integer computations).
ceil(a / b) with Integer Computations
Let's say that we want to compute ceil(a / b). Let's assume for one second that a
is not a multiple of b. ceil(a / b) = a / b + 1
in this case but we'll think differently.
Integer division, as it is specified in C (which is another whole story but we'll simplify things for now), truncates the result.
For example, 3 / 2 = 1.5 with FP division but 1 with integer division.
The most important thing to realize here is that in a / b, if a is not a multiple
of b, the result of the division is like "cutting" a to the previous multiple
of b and then doing the division.
For example, 5/2 = 4/2 and 8/3 = 6/3.
Graphically, it looks like this:
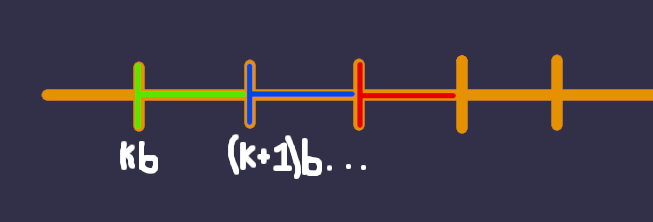
The vertical bars are multiples of some b. All numbers in a same-colored area will have the same result
when divided by b. This is important because, note that when a is not
a multiple, it means it is in some colored area and it is not a vertical bar.
As we said, ceil(a / b) = a / b + 1 i.e. I do the division and then add 1.
But this is the same as taking a and "moving it" to the next
colored area, since any number in the next colored area will be cut in the next vertical bar which effectivelly will
give me +1 in the division. For example, for any a in the blue area (except the vertical bar), I can take the ceil by moving it
anywhere in the red area (including the vertical red) and then doing the division.
"Movement" in this case intuitively means addition. I want to find a number that will move any number in one area to anywhere in the next. I would like this number with which I'm adding to be the same for all numbers because that will make my formula uncoditional and this is good in computers.
Let's think in multiples of 5: |----|----|----| ...
The vertical bars are multiples of 5 and the dashes are the numbers till the next multiple. We want a number t
that will move any dash to the next dashed area and including the next vertical bar.
|----|----|----| ...
For example, I want to move the red dash to anywhere in the green area (and note here that I don't want to move it any further away otherwise I will get a / b + 2 not + 1). I can achieve that by adding to it either 4 (which will get me to the vertical bar) or 5 or 6 or 7 or 8.
This number has to work for all the dashes. All these numbers work for the next of the red except 8 which moves it to the vertical
bar after the green area and we don't want that. So, t must be between 4 and 7 inclusive.
If we do the same reasoning for all the dashes, we'll find that the only t that works for all the dashes
is 4. So, for multiples of 5, t = 4.
If you follow the same reasoning for multiples of any number, you'll find that in general t = b - 1.
And we found this "magic" number that by adding it to a non-multiple a, it gives us the ceil(a / b).
Finally, what happens when a is a multiple of b. In that case, t
can't move it to the next area. Multiples of b are the only numbers which t can't move
to the next area and this is exactly what we want.
All in all, in general ceil(a / b) = (a + b - 1) / b.
To sum up
number_of_iterations = ceil(n - initial_value_of_c / step) =
(n - initial_value_of_c + step - 1) / step
exit_value_of_c = initial_value_of_c + number_of_iterations*step
In general, if you want to look at how a compiler optimizes a piece of code, it's good to get familiar with its Intermediate Representations. The reason for that is that what ends up on assembly is a result of multiple passes, some of which are from the middle-end and some from the back-end. More importantly, the back-end a lot of times obfuscates the code and makes the understanding of the optimization and reasoning of the compiler harder.
In this example we'll see that the middle-end is the one that optimized the loop to a constant computation and the output constant computations happen to have a division. The division is transformed to the standard trick of multiplication and shift by the back end. But, no matter how "standard" this trick is, one might not know it and they'll see some weird multiplications and magic numbers in the output ASM which we'll seem to come out of nowhere. That in turn we'll make it harder for them to understand the actual optimization that in essence had nothing to do with the division.
Don't get me wrong, I love assembly and we should always look at it because this is what is actually executed. But it is not always educational.
Here we'll focus on LLVM and I'll assume familiarity with its basic environment, LLVM IR etc. One standard path I follow to figure out what pass did a particular transformation is the following:
- First of all, compile the C/C++ source code with Clang and tell it output LLVM IR, i.e. usually:
-g0 -emit-llvm -S(note: I use Clang compiled from source which by default outputs IR with better naming. If you have a release build, you can get somewhat better naming by passing it-fno-discard-value-names). - Remove attributes (especially
optnone) and other irrelevant stuff from the output and pass it tooptwith:-sroa. This will convert the code from memory control-flow (i.e. loads / stores) to SSA control-flow (i.e. PHI nodes etc.). It is way more readable that way, plus most optimizations can't work without it. - Pass the output again from
opt, now with the optimization level e.g.-O1but also with the argument-print-after-all. This will print the output IR after every pass and you can identify which pass did what.
In this case, we'll see that most of the job was done by -indvars i.e. IndVarSimplify (Godbolt snippet).
There are some other passes, namely -simplifycfg -instcombine that simplify the code more but the most important
changes are by induction variable simplification.
define i32 @test(i32 %c, i32 %n) {
%0 = icmp sgt i32 %n, %c
%smax = select i1 %0, i32 %n, i32 %c
%1 = add i32 %smax, 2
%2 = sub i32 %1, %c
%3 = udiv i32 %2, 3
%4 = mul nuw i32 %3, 3
br label %while.cond
while.cond: ; preds = %while.body, %entry
br i1 false, label %while.body, label %while.end
while.body: ; preds = %while.cond
br label %while.cond
while.end: ; preds = %while.cond
%5 = add i32 %c, %4 ret i32 %5
}
Let's actually run -simplifycfg(Godbolt snippet)
to remove these dead blocks that have been left from the the while loop.
define i32 @test(i32 %c, i32 %n) {
%0 = icmp sgt i32 %n, %c
%smax = select i1 %0, i32 %n, i32 %c
%1 = add i32 %smax, 2
%2 = sub i32 %1, %c
%3 = udiv i32 %2, 3
%4 = mul nuw i32 %3, 3
br label %while.cond
while.cond: ; preds = %while.body, %entry
br i1 false, label %while.body, label %while.end
while.body: ; preds = %while.cond
br label %while.cond
while.end: ; preds = %while.cond
%5 = add i32 %c, %4
ret i32 %5
}
If we assume for a second that %smax is %n, then LLVM has generated exactly what we computed
above.
%smax is only used to account for the case that we never enter the loop and in this case, the initial value of
c (i.e. %c in LLVM IR) has to be returned. This is a smart trick from LLVM in that,
if it picks the max of n, c. If c is bigger and you plug it in the formula we computed
above, it will be zeroed with the - c and thus number_of_iterations = (step - 1) / step
which is always 0 and thus what we return is the initial value.
At the time of writing this, the whole job is done by rewriteExitValues() that is called in
IndVarSimplify::run(). This is a function that uses LCSSA form to find the exit values of the loop (only those
that are ever used outside of the loop of course) and then uses SCEV to analyze and then rewrite their values.
It's fascinating to see that SCEV has computed the whole expression we came up with into a SCEV expression. The rest of the code basically
turns this expression into code and writes it to the preheader (here entry).