A Beginner's Guide to Vectorization By Hand: Part 2
In this part, we're going to discuss the concept of reduction. Here's the first part of this series. If you know nothing about vectorization, you probably want to take a look at it.
A reduction variable (or simply "reduction")
is an operation that happens in a specfic variable, in every iteration of a loop. It is in the form:
new_value = old_value OP data. That is, in every iteration, the new value
of the variable is an operation involving the old value and some data. Now, the important thing here
is that the OP is the same in every iteration. Furthermore,
for this to make sense, the variable has to have some initial value.
The simplest kind of reduction operation / variable that you have seen is the sum of an array of integers.
int sum_of_array(int *a, int len) { int sum = 0; for (int i = 0; i < len; ++i) sum = sum + a[i]; }
Notice that a reduction is a special kind of a loop-carried dependency. This is when an iteration depends on an earlier one, usually the previous one, which is what happens in reductions since the new value depends on / is computed based on the old value, which was computed in the previous iteration.
In general, when loop-carried dependencies are present, we have a huge problem vectorizing / parallelizing the code because they enforce a sequential order. If the second iteration depends on the first, then the first has to be executed before the second and so we can't execute those two in parallel. But that's what happens with the second and third and inductively, the whole loop has to be executed serially. But reductions are special as you'll see below...
Don't confuse the reduction variables with induction variables. An induction variable is a
variable that gets increased or decreased by a fixed amount on every iteration of a loop
or is a linear function of another induction variable. For example, in the following loop,
i and j are induction variables:
for (int i = 0; i < len; ++i) j = 17 * i; }
i gets increased by a fix amount on every iteration and
j is a linear function of i. Now, to be honest,
I don't know where did the names "induction" and "reduction" come from but it's important to remember
their differences because they're used quite a lot in compiler parlance (especially the induction variables).
Reduction variables are especially interesting when the operation is associative
(like addition or multiplication) because partial values of the final result can be computed
individually (it's even more interesting if it is also commutative, as we'll see below).
For example, let's say we have to sum the integers 1 + 2 + 3 + 4.
Instead of pedantically following this sequential order (i.e., (((1 + 2) + 3) + 4)), we can also do (1 + 2) + (3 + 4),
that is, compute 1 + 2 and 3 + 4 independently and then
add these partial results to get the final result.
When something can be done independently, it is implied that it can be done in parallel. One way to do that is using multi-threading / multi-processing. One other way to do that is using vectorization!
Note that floating-point (FP) addition and multiplication are commutative but not (necessarily)
associative. That is, you can be sure that a + b = b + a but not
that (a + b) + c = a + (b + c). So, the compiler won't generally
do FP optimizations that are based on associativity, unless you tell it that you don't care (e.g. with -ffast-math). Most of the time, you don't care (unless
you're doing e.g. high-precision scientific computing), so you may as well use this flag (which is enabled by default
in some compilers on high levels of optimization).
If you want to parallelize accumulation (or whatever similar operation), I think there are two obvious and intuitive ways to approach. The fisrt is the multi-threading approach. Here the idea is very simple. If we have P threads, and N data, then give N / P data to each thread. That is, if we have P threads, each thread can take an equal (what is equal in general is not as simple as N / P, but this is out of topic) part of the data to handle in parallel. And then they will finish in roughly the 1 / P of the time that would be required for a single thread.
Note: Instead of the term "thread" above, we could also use the term "processor", "node" etc. The point is that we have a system in which more than one instructions can be run in parallel.
Vectorization, however, doesn't work like that. You have only one instruction to run at any point. What you have that is "many" are the lanes. So, how do we take advantage of that ? Well, let's say we want to add the numbers 1, 2, 3, 4, 5, 6, 7, 8, and they're stored in this order in memory. Just put pairs of two in every pair of lanes in (two) vector registers.
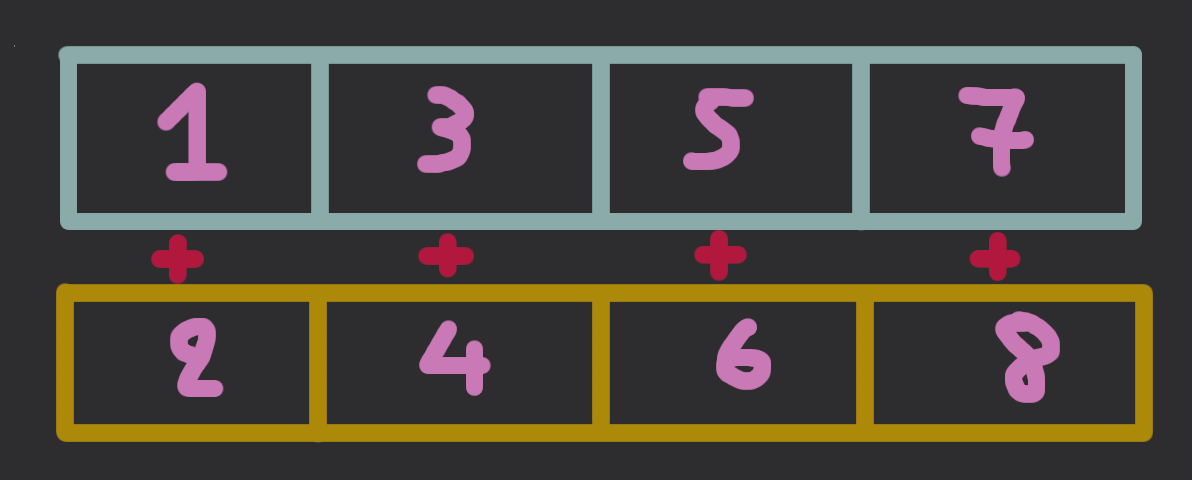
Then, just do normal, element-wise, vectorized addition. This will give us a vector with 4 partial results, which we can add to get the final result.
That's ok but how do you get the data in the lanes ? That is, if I load (the first) 4 values from the array, those will be 1,2,3,4. Then, if I load another 4, I would load the values 5,6,7,8. That doesn't agree with what I described above..
They key insight (which is probably quite intuitive) is that addition is not only associative but also commutative! This means you can change the order of the operands and you'll get the same result i.e. (1+2) + (3+4) + (5+6) + (7+8) = (1+5) + (2+6) + (3+7) + (4+8). The right-hand-side of this is precisely what is convenient for us since is the natural order in
which the data fill the lanes.
Now, for a big array, we start with a register with 0 in all lanes (the initial value). Then we add to it the first 4-packed values. Then we add the output with the next set of 4 values etc. In the final output register, each lane will have a partial result and to get the final result, we just add the four lanes together. Let's see how do we do that in code!
We already know how to load values and do addition of 4-packed values from the previous post, which means that what is basically missing is how to add the 4 lanes of a register. This is an operation that is known as a "horizontal add" (from the obvious visual interpretation) and we'll use the intrinsic _mm_hadd_epi32 for 4-packed 32-bit integer values.
Actually, the horizontal add operation adds the 1st lane to the 2nd and the 3rd to the 4th and saves the two results in the two least significant lanes of the output. We need to repeat another horizontal add to get the final result in the least significant lane of the output.
int add_all_lanes_epi32(__m128i v) { v = _mm_hadd_epi32(v, v); v = _mm_hadd_epi32(v, v); return // Extract least significant lane from `v`; }
Next, we need to learn how do we extract the least significant lane from a register. I know that it would
make a lot of sense to just be able to do v[<lane index>] but remember
that this whole "vectorization" interface with the intrinsics, types and stuff is built over C.
So, if you write that, the C compiler will complain that v is not of array / pointer
type since you can only index arrays and pointers (and you can't overload operators in C, in which case we would
overload [] for __m128i). Fortunately, there's an intrinsic
for our job that again, does not have the easiest-to-remember name: _mm_cvtsi128_si32. I usually wrap it into a function
int get_low_32_bits_si128(__m128i v) { return _mm_cvtsi128_si32(v); }
So, our final function to add all lanes is:
int add_all_lanes_epi32(__m128i v) { v = _mm_hadd_epi32(v, v); v = _mm_hadd_epi32(v, v); return get_low_32_bits_si128(v); }
Now, we're ready to write the whole thing, in the spirit of the previous article:
int sum_of_array(int *A, int len) { int end = (len % 4 == 0) ? len : len - 4; int i = ; __m128i acc = // Register with all lanes equal to 0; for (int i = 0; i < end; i += 4) { __m128i v = loadu_si128(&A[i]); acc = add4(v); } int final_result = add_all_lanes_epi32(acc); for (; i < len; ++i) { final_result += a[i]; } return final_result; }
To finalize that, we need an intrinsic that returns us a register that has all lanes equal to zero: _mm_set1_epi32. Quiz: Why is this named set1 (instead of e.g. set) ? Is there a set0 and if yes, why ?
Just to mention that if we wanted to make a version that handles errors, we would have to handle overflow etc. but those are beside the point.
What we learned in this article is not just how to vectorize accumulation. This is a generic framework to vectorize any reduction operation as long as it fits the precondtions we discussed. In the next article we will examine the peculiarities of vectorizing conditional code!