GJK Algorithm: A Visual Derivation
This is a personally missing intuition on the GJK Algorithm that I hope will help you understand it deeply and follow the related work. A big thanks to Jay Stelly for helping me when I was starting out with this algorithm.
GJK is a collision detection algorithm named after its 3 creators, Gilbert, Johnson and Keerthi. It is quite popular in the game programming world because it enables fast and robust implementation. Besides that, I think it is a very beautful algorithm and one that broadens our algorithmic thinking.
Before we dive into the algorithm, there are a couple of things that it's good to be comfortable with. Namely, convexity and convex hulls. I don't describe them in this article but even if you know nothing about them, you will know enough to read this with a single Google search.
Once upon a time, there was this Minkowski dude who, as an ambitious young boy, had a crazy idea (among many). He said: "I'm going to add shapes together". Enter Minkowski Sums. I'm not sure whether the visual interpretation followed the algebraic definition or vice versa. Either way, we're going to start with the algebraic because it's the boring one, then get to the fun stuff. So, he defined the addition of shapes like this:
C = A + B = {x + y, x ∈ A, y ∈ B}
C is the result of adding the two shapes A and B. To add them, take each point in A and
add it to each point in B. Then all these resulting points form C. For example, if A
has a single point (1, 2) and B has two points (3, 4), (5, 6), then C is the set
of points:
{ (1, 2) + (3, 4), (1, 2) + (5, 6) } = { (4, 6), (6, 8) }
This operation has an interesting visual interpretation. It is like taking one of the two objects and sweeping it around the other object, for example:
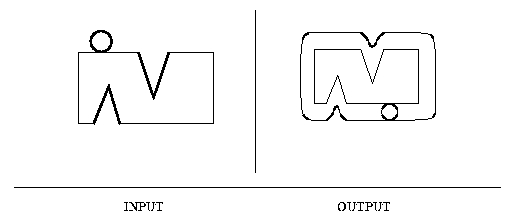
Here you can see that we sweeped the ball around this kind of N.
To make that more concrete, consider adding squares, which is easier, for example these two squares:
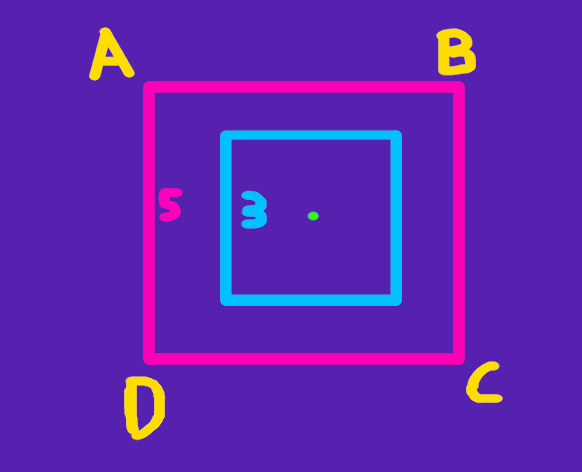
Pretend that the one square's side is 3 and the other's 5 (also pretend they're squares). That will become relevant in a bit. So, to add the blue square to the... I don't know, pink (?) square, take the blue square and move it to each of the vertices of the pink square (A, B, C, D). But move it specifically by aligning its center (which has been drawn green and also happens to be the center of both squares) with each of the vertices of the outer square, like this:
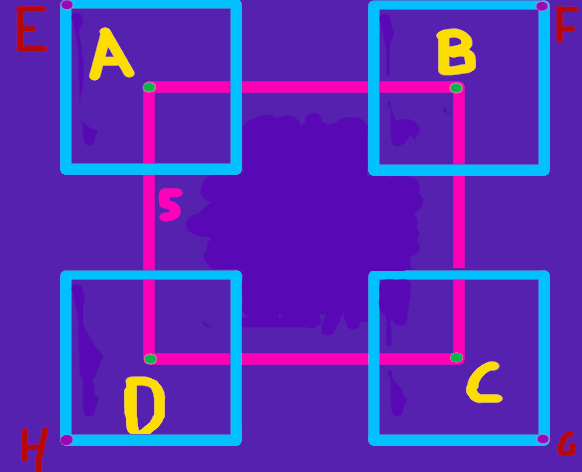
The new, big square which is defined by the vertices E, F, G, H is the Minkowski Sum of the two squares. This new square has a side equal to the sum of the sides of the two squares it came from, that is its side has length 5 + 3 = 8.
Moreover, the Minkoski Sum takes into consideration the disposition of shapes (relative to the origin). Remember that I said that when moving the blue square you should align its center with each of the vertices ? This is because I purposefully drew the squares in such a way so that the center of the squares align with the origin. In general, you move the origin (point (0, 0)) of the shape you add (in this case, the blue square) to each of the vertices of the other shape. See below:

Notice that the square's center is the same as the origin but the circle's center is not, that is, the circle has some disposition relative to the center. Sweeping the circle around the square looks something like this (here I have only moved the circle to one of the vertices):
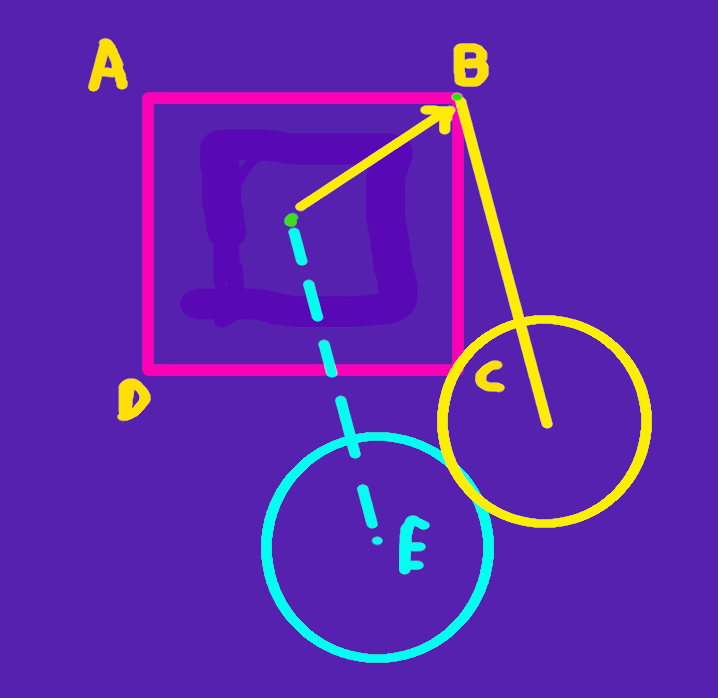
Notice that to move now the circle in the vertices of the square, we move the whole coordinate system of the circle so that the origin of this coordinate system (here it is the green dot and it is not the same as the center of the circle, which is the point E) so that it aligns with each of the vertices. In that way, the Minkowski Sum accounts for this disposition and the final shape is different than if we had the circle's center align with the origin.
So, now that we learned about the Minkowski Sum, let's learn about the Minkowski Difference. This is really a cheat on the Minkowski Sum; instead of adding points, we subtract them, i.e.:
C = A - B = {x - y, x ∈ A, y ∈ B}
Visually this is not much different; we just reflect shape B by the origin (for example, if the shape is in the second quarter of the coordinate system, it will be moved to the fourth). Then, we do the Minkowski Sum.
But why are all these interesting anyway ? Notice that if two objects collide, it means that they have at least one
common point. Which means, that there's a pair
x ∈ A, y ∈ B, such that x = y. That in turn means that
if we subtract them, as part of the Minkowski Difference, we will get the origin (0, 0).
All in all, if the two shapes collide, then the origin will be inside their Minkowski Difference. The whole idea of GJK is to try to deduce whether the origin is in fact inside the Minkowski Difference, but in a very smart way...
So, we could compute the Minkowski Difference, then maybe compute its convex hull or something and then check if the origin is inside. That's all fine, but computing the Minkowski Difference is a O(n2) computation and that's no good. This is supposed to be an algorithm used in real-time collision detection.
All the smartness of GJK is that it tries to figure out if (0, 0) is inside the Minkowski Difference without actually computing it.
So, here's an idea: Let's say that you had a way to compute the furthest point of the Minkowski Difference in a given direction (which is the same as taking the furthest point in the convex hull of the Minkowski Difference). It doesn't matter how we do it for now, let's just assume we can. How can we use that to find whether the origin is inside the Minkowski Difference ?
This is important so let's try to make it crystal clear. You know where the origin is but you don't know the points of the Minkowski Difference. However, you can sort of cheat your way around that problem by asking "give me the furthest point in this direction". Imagine that the points of the Minkowski difference are lights and that you can slowly turn them on one by one by picking a direction and lighting the furthest point in that direction.
Obviously, one could use that by saying "well, try all the different possible directions and you'll eventually get all the points in the convex hull". That's true and having the hull, checking if the origin is inside is trivial. The problem is that the number of directions is infinite. Even if you constrain it to the limits of a computer, say by going +0.00001 every time, still it's a pretty slow way to solve the problem.
We have to be smarter about which directions we choose. Moreover, we can note one important thing: We need at most 3 points to do our job effectively. That is, a smart way to approach the problem is to try to light 3 points that will make up a triangle that encloses the origin. If we do that, we're done.
Let's walk our way through how do we make such a triangle. Starting off, we really know nothing about the Minkowski Difference, we have to pick a random point on it. So, we're picking a random direction and light on our first point. This is what we got and we'll try to do our best with it.
The second point is crucial. We want to go as close to the origin as possible with our second point. For that, we use our procedure that gives us the furthest point towards a direction and as a direction, we pick the opposite of the first point. When I say the opposite, I mean towards the origin. For example, if our first point is (1, 2), this implicitly makes up the vector / direction (1, 2). The opposite of this direction is (-1, -2), the one towards the origin.
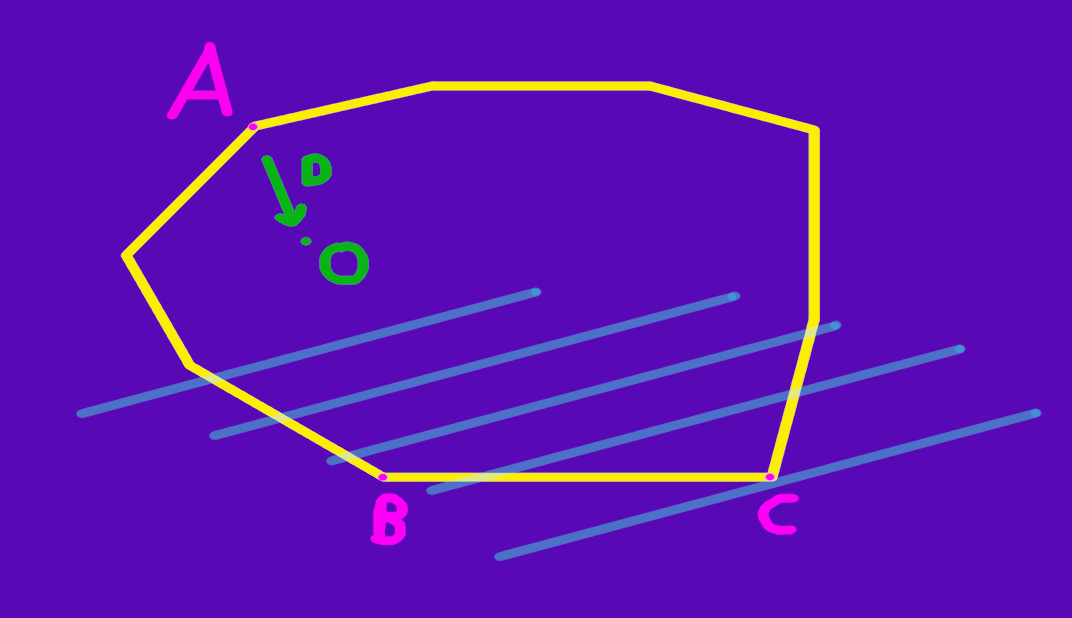
First of all, to be sure we're on the same page: The furthest point in direction D is C not B. It's like we're drawing perpendicular lines relative to the direction (the blue ones here).
Continuing on, the origin is point O. A was our first point and then we're trying to get the furthest point towards the origin, in the direction D.
Notice that now we're in a place to really make a smart decision. We have a line segment, and not just "a line segment". It's a line segment that we tried to maximize towards the origin. For simplicity, check that now basically this line segment leaves the origin at one of two sides. There's the one on the left and then the one the right. Here, the origin is on the left.

The fact that it is on the left is something we can easily determine. And now that we have a side, we can finish our quest for a good triangle. Pick the furthest point towards the side that the origin is in, in order to try to maximize the triangle. That is, pick the point towards the direction that is perpendicular to our line segment and points towards the side of the origin.
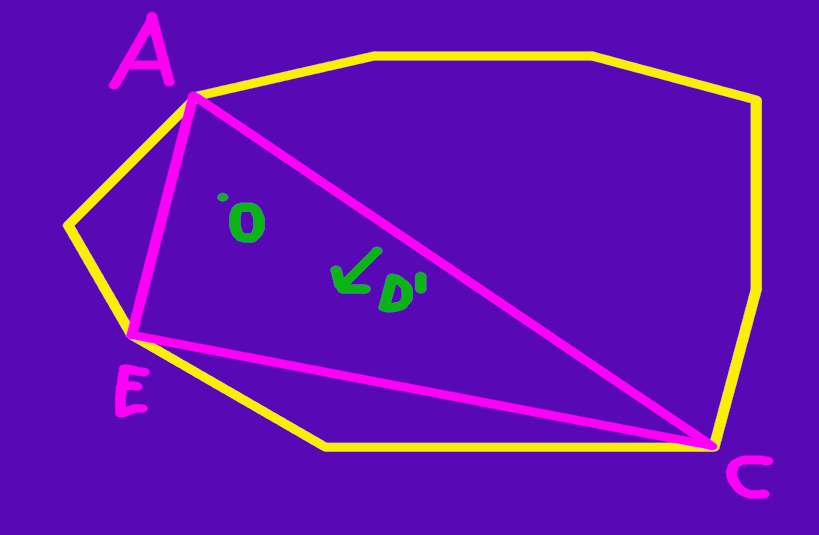
And like magic, we made a triangle that encloses the origin!
That was it for the most important part of this article and it was this intuition that I was missing when I was reading about GJK. Given this intuition I think that it's easy to follow other resources that have already done a good complementary job, some of which I refer in the Related Work at the bottom.
But let me actually do my take on some of the important parts. First of all, the procedure that gives us the furthest point in a direction is called the "support function" or the "support mapping function". This should be a procedure that computes the requested furthest point without knowing the Minkowski Difference and indeed, it is implemented by only knowing the two starting shapes. The idea is actually pretty simple. The furthest point in a direction is the one that maximizes the dot produce with that direction. That is, if we have a shape A and a direction D, the furthest point is the following:
{max(D dot x), x ∈ A}
Now, the key is that the dot product distributes over addition. That is, if you want to find the support mapping of a shape A + B, you can take the support mapping of A + the support mapping of B. In this way you can find the support mapping (furthest point in a direction) in the Minkowski Sum A + B, without actually computing it. Similar reasoning follows for the Minkowski Difference.
Second caveat is that we won't always be able to end up in a triangle that encloses the origin. One reason for that is because the origin might just not be inside the Minkowski Difference. A second reason is that.. err.. basically the procedure can just fail even if it is inside. You can read such cases in the related work. That doesn't mean that we stop, it means that we continue by going back to either a line or a point case (also, the procedure is guaranteed to finish eventually).
Related to the above, the cases where the origin is are not as simplistic as I described them. For example, in the case of a line, we don't split the world in 2 pieces but in 4. Although at the end, if the origin is inside, it will be either on the left or to the right.